Poliedros

Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico πολύεδρον (polyedron), de la raíz πολύς (polys), "muchas" y de έδρα (edra), "base", "asiento", "cara".(tomado de wikipedia)

Poliedro es un cuerpo geométrico cerrado, limitado por caras poligonales.

Elementos de un poliedro

Un poliedro esta compuesto por CARAS, ARISTAS y VÉRTICES. Observa las siguientes imagenes: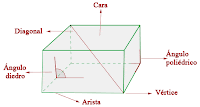

En todos los poliedros convexos o regulares se verifica (fórmula de Euler) siempre que:

Nº de caras + Nº de vértices = Nº de aristas + 2.

Tipos de poliedros

Poliedros Regulares.

Los poliedros regulares son los que tienen sus vértices iguales y todas sus caras formadas por polígonos regulares iguales. Este grupo de poliedros ya era conocido por Euclides (330 a.C.) y estos cinco sólidos estuvieron acompañados de cierto misticismo. Se asociaban con los cuatro elementos supuestos y con el Universo y reciben el nombre de sólidos platónicos. Los únicos poliedros regulares son:

TETRAEDRO Formado por cuatro triángulos equiláteros. (Tetra en griego significa cuatro y edro cara.) Es el que tiene menor volumen de los cinco en comparación con su superficie.

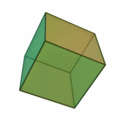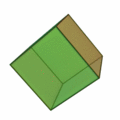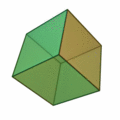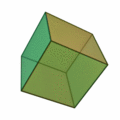
CUBO o HEXAEDRO Formado por seis cuadrados. (Hexa significa seis). Permanece estable sobre su base.

OCTAEDRO Formado por ocho triángulos equiláteros. Gira libremente cuando se sujeta por vértices opuestos.

DODECAEDRO Formado por doce pentágonos regulares. (Dodeca significa doce).

ICOSAEDRO Formado por veinte triángulos equiláteros. (Icosa significa veinte).

Resumen:

Tetraedrocaras = 4vértices = 4aristas = 6

4 + 4 - 6 = 2

orden = 3

Cubo o Hexaedro caras = 6vértices = 8aristas = 12

6 + 8 - 12 = 2

orden = 3

Octaedro

caras = 8vértices = 6aristas = 12

8 + 6 - 12 = 2

orden = 4

Dodecaedrocaras = 12vértices = 20aristas = 30

12 + 20 - 30 = 2

orden = 3

Icosaedrocaras = 20vértices = 12aristas = 30

20 + 12 - 30 = 2

orden = 5

Poliedros Irregulares

Poliedro definido por polígonos que no son todos iguales.

Prismas

Un prisma es un poliedro limitado por dos polígonos iguales y paralelos en las bases y paralelogramos en las caras laterales.

Clasificación de prismas

Atendiendo a sus bases: En función del polígono de las bases, los prismas pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.
Atendiendo a su inclinación: Si las caras laterales son perpendicualres a las bases (son rectángulos), el prisma es recto, si no , es oblicuo.

prisma recto: el eje es perpendicular a los polígonos base,
prisma oblicuo: el eje no es perpendicular a los polígonos base,
prisma regular: las bases son poligonos regulares,
- prisma regular recto: las bases son poligonos regulares y el eje es perpendicular a los polígonos base.
- prisma regular oblicuo: las bases son poligonos regulares y el eje no es perpendicular a los polígonos base.
paralelepipedo: prisma cuyas bases son paralelogramos. Pueden ser a su vez rectos u oblicuos

Más prismas: www.vitutor.net/2/2/21.html

Piramides

Poliedro definido por un polígono base y cuyas caras laterales son triángulos que poseen un vértice común, denominado vértice de la pirámide, que no está contenido en el plano base. La recta que pasa por el vértice de la pirámide y el centro geométrico de la base se denomina eje de la pirámide. Las pirámides se clasifican en:

pirámide recta: el eje es perpendicular al polígono base,
pirámide oblicua: el eje no es perpendicular al polígono base,
pirámide regular: la base es un poligono regular,
- pirámide regular recta: la base es un poligono regular y el eje es perpendicular al polígono base.
- pirámide regular oblicua: la base es un poligono regular y el eje no es perpendicular al polígono base.

Software

Tenemos un programita que te ayudara a poder aprender más de los poliedros: descargar
para ver mas programas puedes ver el siguiente enlace: www.peda.com/download/

Elaboración de Poliedros

Dale Click en al imagen de la derecha para ver más grande