Esta entrada es un recopilación de varias páginas y la principal: gaussianos.com
Una ecuación diofántica es una ecuación cuyas soluciones son números naturales.



 La ecuación queda:
La ecuación queda:
 Haciendo cuentas nos queda lo siguiente:
Haciendo cuentas nos queda lo siguiente:
 Si estabais pensando que nos iba a quedar un sistema de ecuaciones
sencillo de resolver estáis equivocados. Nos ha quedado una única
ecuación con dos incógnitas. ¿Nos faltan datos? No. Podemos resolverla.
Bienvenidos al maravilloso mundo de las ecuaciones diofánticas.
Si estabais pensando que nos iba a quedar un sistema de ecuaciones
sencillo de resolver estáis equivocados. Nos ha quedado una única
ecuación con dos incógnitas. ¿Nos faltan datos? No. Podemos resolverla.
Bienvenidos al maravilloso mundo de las ecuaciones diofánticas.
 con
con  .
.
1.- Comenzamos con la implicación de izquierda a derecha:
Si la ecuación
 (1)
tiene solución entera, entonces existen
(1)
tiene solución entera, entonces existen  tales que
tales que 
Como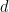 es un divisor común de
es un divisor común de  y
y 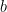 , entonces
, entonces  y
y  , con
, con  .
.
Tenemos entonces lo siguiente:

 De donde obtenemos
De donde obtenemos
 Con lo que hemos llegado a que
Con lo que hemos llegado a que  y
y  son soluciones de la ecuación (1).
son soluciones de la ecuación (1).
Entonces:

Si es solución de la ecuación (1), entonces se cumple que
es solución de la ecuación (1), entonces se cumple que  . Pero entonces las expresiones de (2) también son solución de dicha ecuación:
. Pero entonces las expresiones de (2) también son solución de dicha ecuación:
 Faltaría ver entonces que todas las soluciones de (1) son de la forma que hemos descrito en (2). A por ello vamos:
Faltaría ver entonces que todas las soluciones de (1) son de la forma que hemos descrito en (2). A por ello vamos:
Partiendo de la solución particular anterior , supongamos que tenemos una solución
, supongamos que tenemos una solución  de la ecuación diofántica lineal (1). Tenemos entonces las dos ecuaciones siguientes:
de la ecuación diofántica lineal (1). Tenemos entonces las dos ecuaciones siguientes:
 Restamos las dos ecuaciones, obteniendo
Restamos las dos ecuaciones, obteniendo
 Pasando el segundo sumando al otro miembro de la igualdad llegamos a
Pasando el segundo sumando al otro miembro de la igualdad llegamos a
 (3)
Dividimos ahora por
(3)
Dividimos ahora por 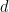 :
:
 Como
Como  y
y  son números enteros primos relativos (ya que al dividirlos entre su
máximo común divisor les hemos quitado los factores que tuvieran en
común en un principio), y
son números enteros primos relativos (ya que al dividirlos entre su
máximo común divisor les hemos quitado los factores que tuvieran en
común en un principio), y  divide a
divide a  , debe cumplirse que
, debe cumplirse que  divida a
divida a  .
.
Esto nos lleva a que debe existir tal que:
tal que:
 De donde obtenemos que
De donde obtenemos que  debe ser de la forma:
debe ser de la forma:
 , con
, con  Sustituyendo este valor de
Sustituyendo este valor de  en la ecuación (3) llegamos, después de unos sencillos cálculos, a la expresión buscada para
en la ecuación (3) llegamos, después de unos sencillos cálculos, a la expresión buscada para  :
:

 Vamos a ver si somos capaces de encontrar cuántos trajes de cada color compró este señor.
Vamos a ver si somos capaces de encontrar cuántos trajes de cada color compró este señor.
Como es un divisor de
es un divisor de  nuestra ecuación tiene soluciones. Para obtener
nuestra ecuación tiene soluciones. Para obtener  y
y  debemos utilizar el algoritmo de Euclides para el cálculo del máximo común divisor junto con la identidad de Bezout, citada anteriormente. En este caso se obtiene
debemos utilizar el algoritmo de Euclides para el cálculo del máximo común divisor junto con la identidad de Bezout, citada anteriormente. En este caso se obtiene
 por lo que
por lo que  y
y  .
.
Entonces la solución particular queda de la siguiente forma:
 A partir de esto ya es sencillo encontrar todas las soluciones:
A partir de esto ya es sencillo encontrar todas las soluciones:

 Por tanto, los únicos valores posibles para
Por tanto, los únicos valores posibles para  son
son  .
.
Fuente de la demostración:
En este caso la ecuación tiene un número finito de soluciones o ninguna.
Resolución:
ax = c - by
Dando valores a y, desde y = 0 hasta y = a - 1, encontraremos un único valor que sea múltiplo de a.
Sea b el valor de y que hace c - by múltiplo de a. Entonces conoceremos el valor de x que satisface la ecuación. Sea a ese valor.
Para obtener las demás soluciones hacemos x = a - bt e y = b +at y damos a valores a t = 0,1,2... siempre que se pueda hacer la sustracción.
Sea la ecuación 3x + 5y = 52
3x = 52 - 5y.
Para y = 0 queda 3x = 52
Para y = 1 queda 3x = 47
Para y = 2 queda 3x = 42
El único valor de y que hace x entero es y = 2. Entonces b = 2 y a = 14.
x = 14 - 5t. Para t = 0, x = 14. Para t = 1, x = 9. Para t = 2, x = 4.
y = 2 + 3t. Para t =0, y = 2. Para t = 1, y = 5. Para t = 2, x = 8
En este caso la ecuación tiene un número infinito de soluciones.
Resolución:
ax = c + by
Dando valores a y, desde y = 0 hasta y = a - 1, encontraremos un único valor que sea múltiplo de a.
Sea b el valor de y que hace c + by múltiplo de a. Entonces conoceremos el valor de x que satisface la ecuación. Sea a ese valor.
Para obtener las demás soluciones hacemos x = a + bt e y = b +at y damos a valores a t = 0,1,2... siempre que se pueda hacer la sustracción.
Ahora hacemos a = bc.
b y c deben ser ambos pares o ambos impares, pues la suma de dos números y su diferencia son ambas pares o ambas impares. Entonces
x - y = b
x + y = c
Resolviendo el sistema se obtiene:
x = (b - c) / 2
y = (b + c) / 2
Suponemos x impar, lo podemos hacer ya que al ser x, y, z primos entre sí no pueden haber dos pares.
Transformamos la ecuación en z2 - y2 = x2
Como z2 - y2 = (z - y)(z + y).
(z - y)(z + y) = x2
El problema se reduce a descomponer x2 como producto de dos números primos entre sí. Sean u y v estos números.
(z - y)(z + y) = uv obtenemos y = (u2 - v2)/2, z = (u2 + v2)/2
Son dos soluciones enteras puesto que la suma y la diferencia de dos impares es un número par.
Lagrange demostró que la enésima solución (xn, yn), se puede expresar en términos de la primera de esta forma:
xn + ynÖd = (x1 + y1Öd)n
Resolver la ecuación de Pell significa encontrar x1 e y1.
Hay un método bastante rápido que consiste en expresar la raíz como una fracción continua.
Sea la ecuación x2 = 14y2 + 1
Ö14 = 3 + 1/(1 + (1/(2 +1)) = 15/4; x1 = 15, y1 = 4
(15 + 4Ö14)2 = 449 + 120Ö14 ; x2 = 449, y2 = 120
(15 + 4Ö14)3 = 13455 + 3596Ö14 ; x3 = 13455, y3 = 3596
Con a cualquier número natural.
Su representación gráfica es una curva elíptica en el plano Real. Para cada a posee un número finito de soluciones enteras.
Expresado en palabras significa que un cubo no se puede expresar como suma de dos cubos, y ninguna potencia mayor o igual que tres se puede expresar como suma de otras dos similares.
Este teorema estuvo sin demostrar durante más de trescientos años, aunque Fermat anotó en el margen del libro de Aritmética de la edición de Bachet "Para esto he descubierto una demostración verdaderamente maravillosa, pero el margen de éste libro es demasiado pequeño para contenerla...". Nadie encontró esa demostración y se dudó de su existencia.
El intento por demostrar éste teorema ocasionó una evolución de las matemáticas.
Finalmente en 1993 Andrew Wiles demostró el teorema relacionándolo con las curvas elípticas modulares, en un manuscrito de doscientos folios.
x + y + z = 100
50x + 1000y + 5000z = 100000
Simplificando y sustituyendo el valor de x obtenido en la primera ecuación nos queda:
x + y + z = 100
19y + 99z = 1900
Despejando y en la segunda ecuación nos queda y = 100 - 99z/19. Sustituyendo este valor en la primera ecuación y despejando x nos queda: x = 88z/19.
Para que los valores de x, y y z sean enteros z tiene que ser múltiplo de 19.
si z = 19, y = 1 y x = 80.
Leer más...
Historia
Las ecuaciones diofánticas deben su nombre a Diofanto que fue quien las estudió primero.Una ecuación diofántica es una ecuación cuyas soluciones son números naturales.
Ecuaciones de la forma ax + by = c
Motivación
Supongamos que nos encontramos el siguiente problema:Un hombre va a una tienda de ropa y compra 12 trajes, unos negros y otros grises, por 1200 €. Si los trajes negros valen 30 € más que los grises y ha comprado el mínimo posible de estos últimos, ¿cuántos trajes ha comprado de cada color?Vamos a plantearlo:
Ecuaciones diofánticas
Una ecuación diofántica es una ecuación algebraica
en la que aparecen varias variables cuyas soluciones son números
enteros. Es decir, resolver una ecuación diofántica consiste en
determinar qué números enteros la cumplen. Su nombre lo toman del
matemático Diofanto de Alejandría, quien, además de ser
uno de los primeros en utilizar simbolismo en álgebra, se dedicó entre
otras cosas al estudio de estas ecuaciones
Las ecuaciones diofánticas del tipo anterior se denominan ecuaciones diofánticas lineales.
Este caso particular de este tipo de ecuaciones es el que vamos a
aprender a resolver en este artículo. Más concretamente, vamos a mostrar
(y demostrar) un método para calcular las soluciones enteras de la
ecuación
Existencia de soluciones
El primer resultado que vamos a ver y demostrar tiene que ver con la existencia de soluciones de estas ecuaciones. Vamos con él:Teorema:Demostración:
Una ecuación lineal diofántica de la formatiene solución entera
si y sólo si el máximo común divisor de
y
es un divisor de
.
Además, si llamamosal
se tiene que una solución particular de dicha ecuación puede obtenerse de la siguiente forma:
siendo.
1.- Comenzamos con la implicación de izquierda a derecha:
Si la ecuación
Como
Tenemos entonces lo siguiente:
Es decir, nos queda una expresión del tipo  , con todos ellos números enteros. En consecuencia tanto
, con todos ellos números enteros. En consecuencia tanto 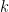 como
como 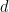 deben dividir a
deben dividir a  , concluyendo así esta parte de la demostración.
, concluyendo así esta parte de la demostración.
2.- Vamos ahora con la implicación de derecha a izquierda, obteneidno como bonus el además:
Supongamos ahora que 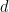 es un divisor de
es un divisor de  . Entonces existe
. Entonces existe  tal que
tal que  . Por otra parte, por el teorema de Bezout existen
. Por otra parte, por el teorema de Bezout existen  tales que
tales que  . Multiplicamos los dos miembros de esta igualdad por
. Multiplicamos los dos miembros de esta igualdad por 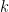 :
:
Entonces:
es una solución de la ecuación (1), que es lo que queríamos demostrar.
Lo que hemos conseguido hasta ahora es saber reconocer qué ecuaciones
diofánticas lineales tienen soluciones y calcular una solución
particular de las mismas. Pero queremos una solución general, es decir,
todas las soluciones de las ecuaciones diofánticas lineales que se
puedan resolver. A ello vamos en el siguiente punto.
Solución general de una ecuación diofántica lineal
Vamos a demostrar el siguiente teorema:Teorema:Demostración:
Sies una solución particular de la ecuación
entonces todas las soluciones enteras(1)
de la misma son de la forma:
con(2)
, siendo
.
Si
Partiendo de la solución particular anterior
Esto nos lleva a que debe existir
Ejemplo práctico
Volvamos a nuestro amigo el de los trajes. Nos quedamos en la ecuación diofántica lineal siguiente:Como
Entonces la solución particular queda de la siguiente forma:
En principio estas expresiones nos dan todas las soluciones del
problema, pero todavía no hemos terminado. Hay que tener en cuenta más
cosas. Analizando los datos obtenidos sabemos que el número de trajes
negros que ha comprado es  , por lo que el número de trajes grises comprados es
, por lo que el número de trajes grises comprados es  .
.
Teniendo en cuenta que el número de trajes de cada tipo comprados por
nuestro amigo debe ser positivo y menor que 12 se tiene lo siguiente:
Pero el enunciado también decía que ha comprado el mínimo número de
trajes grises posibles. Probando con los valores anteriores esta
condición se cumple para  . En consecuencia el protagonista de nuestro problema compró
. En consecuencia el protagonista de nuestro problema compró  trajes grises y
trajes grises y  trajes negros.
trajes negros.
Fuente de la demostración:
- Álgebra y Matemáticas Discretas I, de Carmen Moreno Valencia.
En resumen para todas las formas:
Ecuaciones de la forma ax + by = c
Para que ésta ecuación tenga solución c tiene que ser divisible por el máximo común divisor de a y b.En este caso la ecuación tiene un número finito de soluciones o ninguna.
Resolución:
ax = c - by
Dando valores a y, desde y = 0 hasta y = a - 1, encontraremos un único valor que sea múltiplo de a.
Sea b el valor de y que hace c - by múltiplo de a. Entonces conoceremos el valor de x que satisface la ecuación. Sea a ese valor.
Para obtener las demás soluciones hacemos x = a - bt e y = b +at y damos a valores a t = 0,1,2... siempre que se pueda hacer la sustracción.
Sea la ecuación 3x + 5y = 52
3x = 52 - 5y.
Para y = 0 queda 3x = 52
Para y = 1 queda 3x = 47
Para y = 2 queda 3x = 42
El único valor de y que hace x entero es y = 2. Entonces b = 2 y a = 14.
x = 14 - 5t. Para t = 0, x = 14. Para t = 1, x = 9. Para t = 2, x = 4.
y = 2 + 3t. Para t =0, y = 2. Para t = 1, y = 5. Para t = 2, x = 8
Ecuaciones de la forma ax - by = c
Para que ésta ecuación tenga solución c tiene que ser divisible por el máximo común divisor de a y b.En este caso la ecuación tiene un número infinito de soluciones.
Resolución:
ax = c + by
Dando valores a y, desde y = 0 hasta y = a - 1, encontraremos un único valor que sea múltiplo de a.
Sea b el valor de y que hace c + by múltiplo de a. Entonces conoceremos el valor de x que satisface la ecuación. Sea a ese valor.
Para obtener las demás soluciones hacemos x = a + bt e y = b +at y damos a valores a t = 0,1,2... siempre que se pueda hacer la sustracción.
Ecuaciones de la forma x2 - y2 = a
Como x2 - y2 = (x+y).(x-y). La ecuación queda (x-y).(x+y) = a.Ahora hacemos a = bc.
b y c deben ser ambos pares o ambos impares, pues la suma de dos números y su diferencia son ambas pares o ambas impares. Entonces
x - y = b
x + y = c
Resolviendo el sistema se obtiene:
x = (b - c) / 2
y = (b + c) / 2
Ecuaciones de la forma x2 + y2 = z2
Supondremos x, y, z primos entre sí ya que si x, y ,z es solución de la ecuación también lo es a.x, a.y, a.z para cualquier a .De ahí se deduce que encontrada una solución hay infinitas.Suponemos x impar, lo podemos hacer ya que al ser x, y, z primos entre sí no pueden haber dos pares.
Transformamos la ecuación en z2 - y2 = x2
Como z2 - y2 = (z - y)(z + y).
(z - y)(z + y) = x2
El problema se reduce a descomponer x2 como producto de dos números primos entre sí. Sean u y v estos números.
(z - y)(z + y) = uv obtenemos y = (u2 - v2)/2, z = (u2 + v2)/2
Son dos soluciones enteras puesto que la suma y la diferencia de dos impares es un número par.
Ecuaciones de la forma x = dy2 + 1
Esta ecuación, con d un número natural mayor que cero, se llama ecuación de John Pell, aunque fue Lagrange quien resolvió la ecuación.Lagrange demostró que la enésima solución (xn, yn), se puede expresar en términos de la primera de esta forma:
xn + ynÖd = (x1 + y1Öd)n
Resolver la ecuación de Pell significa encontrar x1 e y1.
Hay un método bastante rápido que consiste en expresar la raíz como una fracción continua.
Sea la ecuación x2 = 14y2 + 1
Ö14 = 3 + 1/(1 + (1/(2 +1)) = 15/4; x1 = 15, y1 = 4
(15 + 4Ö14)2 = 449 + 120Ö14 ; x2 = 449, y2 = 120
(15 + 4Ö14)3 = 13455 + 3596Ö14 ; x3 = 13455, y3 = 3596
Ecuaciones de la forma y2 = x3 + a
Esta ecuación con a, número natural, se llama ecuación de Louis Mordell.Con a cualquier número natural.
Su representación gráfica es una curva elíptica en el plano Real. Para cada a posee un número finito de soluciones enteras.
Ecuaciones de la forma xn + yn = zn
La ecuación xn + yn = zn no tiene solución para n > 3, siendo n un número entero.Expresado en palabras significa que un cubo no se puede expresar como suma de dos cubos, y ninguna potencia mayor o igual que tres se puede expresar como suma de otras dos similares.
Este teorema estuvo sin demostrar durante más de trescientos años, aunque Fermat anotó en el margen del libro de Aritmética de la edición de Bachet "Para esto he descubierto una demostración verdaderamente maravillosa, pero el margen de éste libro es demasiado pequeño para contenerla...". Nadie encontró esa demostración y se dudó de su existencia.
El intento por demostrar éste teorema ocasionó una evolución de las matemáticas.
Finalmente en 1993 Andrew Wiles demostró el teorema relacionándolo con las curvas elípticas modulares, en un manuscrito de doscientos folios.
Sistemas de ecuaciones
Supongamos que tenemos que resolver este sistema de ecuaciones, sabiendo que las soluciones tienen que ser números naturalesx + y + z = 100
50x + 1000y + 5000z = 100000
Simplificando y sustituyendo el valor de x obtenido en la primera ecuación nos queda:
x + y + z = 100
19y + 99z = 1900
Despejando y en la segunda ecuación nos queda y = 100 - 99z/19. Sustituyendo este valor en la primera ecuación y despejando x nos queda: x = 88z/19.
Para que los valores de x, y y z sean enteros z tiene que ser múltiplo de 19.
si z = 19, y = 1 y x = 80.





