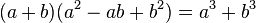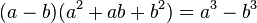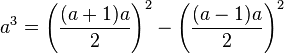Para poder ver la version de descargar ingresa al liguiente link
Factor común
El resultado de multiplicar un binomio a+b con un término c se obtiene aplicando la propiedad distributiva: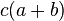 (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).
(el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).
- Ejemplo

Binomio al cuadrado o cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Es decir: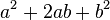 , se conoce como trinomio cuadrado perfecto.
, se conoce como trinomio cuadrado perfecto.Cuando el segundo término es negativo, la ecuación que se obtiene es:
- Ejemplo

Producto de dos binomios con un término común
Cuando se multiplican dos binomios que tienen un término común, se suma el cuadrado del término común con el producto el término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.- Ejemplo

Producto de dos binomios conjugados
Dos binomios conjugados son aquellos que sólo se diferencien en el signo de la operación. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados
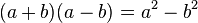
- Ejemplo

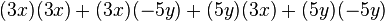
Polinomio al cuadrado
Para elevar un polinomio con cualquier cantidad de términos, se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.- Ejemplo
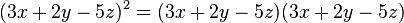
Binomio al cubo o cubo de un binomio
Para calcular el cubo de un binomio, se suma: el cubo del primer término, con el triple producto del cuadrado del primero por el segundo, más el triple producto del primero por el cuadrado del segundo, más el cubo del segundo término.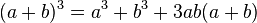
- Ejemplo
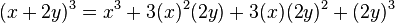
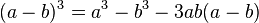
- Ejemplo

Identidad de Argand
Identidades de Gauss
Identidades de Legendre
Identidades de Lagrange
Otras identidades
Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique cuales productos son los únicos que pueden llamarse notables y los demás no. Existen otras fórmulas, que aunque menos usadas que las anteriores, pueden en cierto contexto ser consideradas productos notables. Entre ellas se destacan:- adicion de cubos

- diferencia de cubos

- Suma de potencias n-ésimas
- Sí y sólo si "n" es impar,
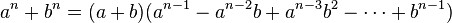
- Diferencia de potencias n-ésimas
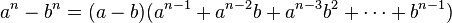
Existe una ingeniosa fórmula para representar un cubo como suma de dos cuadrados:
Un resumen de los principales productos notables:
Producto notable | Expresión algebraica | Nombre | |
| (a + b)2 | = | a2 + 2ab + b2 | Binomio al cuadrado |
| (a + b)3 | = | a3 + 3a2b + 3ab2 + b3 | Binomio al cubo |
| a2 - b2 | = | (a + b) (a - b) | Diferencia de cuadrados |
| a3 - b3 | = | (a - b) (a2 + b2 + ab) | Diferencia de cubos |
| a3 + b3 | = | (a + b) (a2 + b2 - ab) | Suma de cubos |
| a4 - b4 | = | (a + b) (a - b) (a2 + b2) | Diferencia cuarta |
| (a + b + c)2 | = | a2 + b2 + c2 + 2ab + 2ac + 2bc | Trinomio al cuadrado |
productos notables






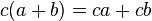
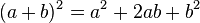
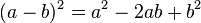
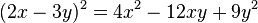
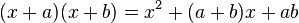
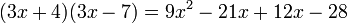

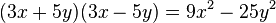

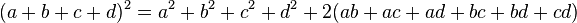
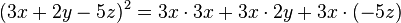
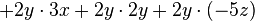

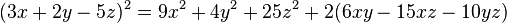
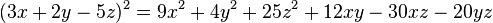
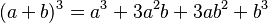

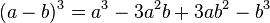

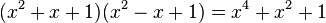

![a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)[(a-b)^2+(b-c)^2+(a-c)^2] \,](http://upload.wikimedia.org/math/e/c/e/ece4c9a9affcf9ddde6f469607ee421b.png)